64th anniversary tablecloth I: theory

In my last post (two months ago!), I asked for ideas for a tablecloth that would feature 8 squares for my grandparents' 64th (8 sqared-th) anniversary. A twitter friend pointed me to Wooly Thoughts, a site with the tag line "in pursuit of crafty mathematics," and I ended up really liking this design. My version has 8 squares in it, of course. I used more math than I'm usually aware of using when I sew, and it was really fun. In this post, I'll talk about some of the math I used. In the next post, I'll talk about the actual construction of the tablecloth.

The mathematics behind the square pattern is a curve of pursuit, at least as I understand it. I haven't done the computations myself, but I think that the "spiral" (it's piecewise straight, but the mind easily makes it into a curved spiral) traced out by the corners of the squares represents the path four dogs (or mice) would take if they were all mutually chasing each other at constant speed. Pretty cool, huh? The way I thought of constructing it was just rotating a smaller square until its corners hit the sides of the next larger square.

I decided that I wanted a constant ratio of sizes of squares, and I thought that it would be cool if the innermost square were parallel with the outermost. I did a simple high school geometry proof to make sure that the angle of successive squares was additive.

The left picture is a schematic of a few of the squares. The right is a blow-up of the way the angles in question are situated. The variable x represents the amount of rotation at each layer. The variable y represents the total rotation after two layers. I used the fact that the sum of angles of a Euclidean triangle is 180 degrees and that vertical angles are congruent to conclude that y=2x, which means that rotation is additive. (OK, technically I showed that the rotation would be additive if the rotation is by the same amount each time, but if x were replaced with z for a different amount of rotation, we would find that y=x+z.)

There might be an easier way to see that rotation would be additive in this case. It's obvious that it is additive if the vertices of both angles x are in the same place, so if the squares all had a corner in common. But I was worried that maybe something weird would happen when you slid the second angle along the side of the first triangle. This proof told me that nothing weird would happen. I have learned that my intuition is often wrong in math, so it was nice to have a proof so I knew for sure.

Since 13x7=91, which is close to 90, I decided that each square should be rotated by about 13 degrees to get the sides of the last square to be parallel with the first. I wanted the tablecloth to have a diagonal length of 60 inches because my vision was for it to be rotated and put on their table diagonally, and based on their table size, I thought 60 inches was a good length.

I couldn't actually find our calculator. (Update: I found it recently when I accidentally knocked it off the back of the work desk. But the batteries are dead anyway.) Instead, I used the google as a calculator to figure out what the side length of the largest square should be to give diagonal length 60. (Answer: 60/sqrt(2), about 42.4 inches, conveniently about the same as the width of the orange fabric I was using.)
 Then I set up an equation to figure out the ratio between successive square side lengths. In the picture to the left, I assume the total side length of the largest square is 1 and figure out where the second square touches the first using the equation I wrote at the bottom. To figure out the side length of the smaller square, I used the Pythagorean theorem with the x and 1-x to get the hypotenuse of that triangle, which is the side length of the second square. After getting a decimal approximation of that side length, I computed all the square side lengths to three significant figures. That should have been my first clue that I was greatly underestimating the difference between theory and practice: my tape measure goes down to 16ths of an inch, and my cutting is considerably less accurate than my tape measure.

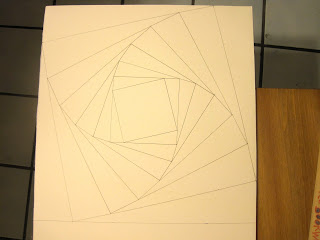
Here is a sketch of my plan on poster board.

Even with the relatively good precision of pencil and paper, the innermost square didn't line up very well with the outermost square. But it looked cool anyway.

Unfettered by banal practicalities such as the realistic amount of precision I could hope for when cutting the fabric, I double-checked my numbers and went off to cut the fabric.

Tune in tomorrow (or whenever I get around to posting again) to read about the differences between theory and practice that I encountered during this project! (Compelling cliffhanger, or most compelling cliffhanger?)